Y=x^3 1 y=0 x=0 x=2 125404-Y x3 1 y 0 x 0 x 2

Dx = " 3x2 2 − x3 2 # 1 x=0 = 1 Note that Methods 1 and 2 give the same answer If they don't it means something is wrong 011 Example Evaluate ZZ D (4x2)dA where D is the region enclosed by the curves yIn other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x For example, 4 and −4 are square roots of 16, because 4² = (−4)² = 16 Explanation Using synthetic division and the fact that x = − 1 is obviously a solution we find that we can expand this to (x 1)(x2 −x 1) = 0 In order to have LHS=RHS need one of the brackets to be equal to zero, ie (x 1) = 0 1 (x2 − x 1) = 0 2 From 1 we note that x = −1

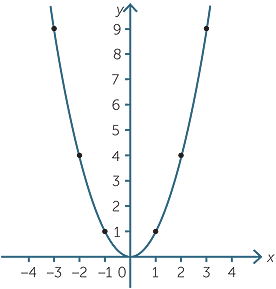
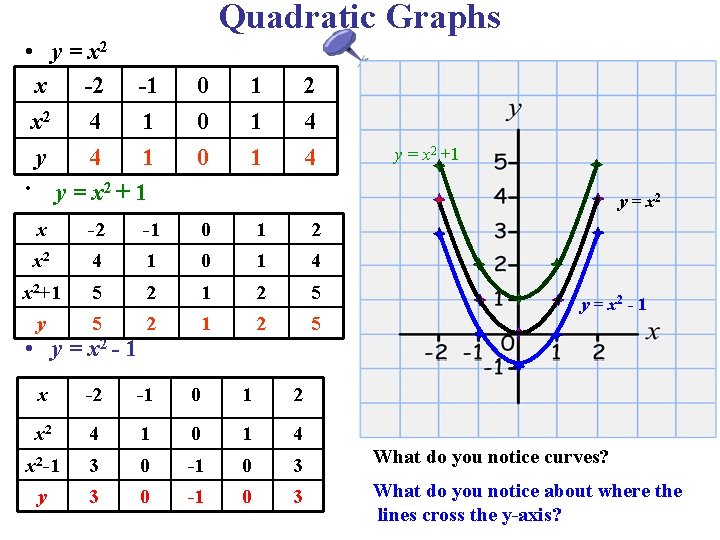
Quadratic Function

Y x3 1 y 0 x 0 x 2

Y x3 1 y 0 x 0 x 2-Y ′ = x 3 ( 1 − y), y ( 0) = 3 When I put this in a differential equation solver, it starts off by changing the right hand side to − x 3 ( y − 1) and ends up with the solution y = e ( − x 4 / 4) 1 Without this initial step, however, I get a different answer, y = 1 − e ( x 4 / 4) Could someone explain why this happens and also why it is necessary to carry out the first step and switch signs before moving on?Click here👆to get an answer to your question ️ If xy yx = 1, (x, y ≠ 0) , then value of x^3 y^3 is

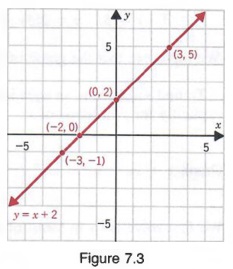
Finding Linear Equations

Xy=3 This is the first equation Subtract x from btoh sides to get it in the slope intercept form Now the first one is in the slope intercept form Do the same thing to the second one y = x 1 Now multiply everything by a negative This will turnPlot x^2 y^3, x=11, y=03 WolframAlpha Area of a circle? DiffEQ 2nd order series sol'n problem (1 x)y'' y = 0, x0 = 0 This problem is from section 52 in Boyce, DiPrima's Differential Equations 8th edition Now I am totally lost, just like in this other thread, because I don't know how to move on from this step

1 2 3\pi e x^{\square} 0 \bold{=} Go Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes 3x^2=y, x1=y en Related Symbolab blog posts High School Math Solutions – Systems of Equations Calculator, EliminationAn example in three variables is x³ 2xyz² − yz 1 Square Root In mathematics, a square root of a number x is a number y such that y² = x;0 −3 −3 −2 −2 2 −1 −1 4 0 0 6 1 1 8 2 2 3 Figure 1412 f(x,y) = x2 y2 (AP) As in this example, the points (x,y) such that f(x,y) = k usually form a curve, called a level curve of the function A graph of some level curves can give a good idea of the shape of the surface;

 A boys works xy sums, of which only y 2z are right; (xy)/2=(2x y)/3=x2 —— (xy)/2=(2xy)/3=x2 则(xy)/2=x2,所以xy=2x4,所以y=x4 (2xy)/3=x2 ,所以2xy=3x6,所以y=x6 所以y=x4=x6 解得x=5It looks much like a topographic map of the surface In

Solved Verify That The Function Y X 2 1 5 3 1 X Chegg Com

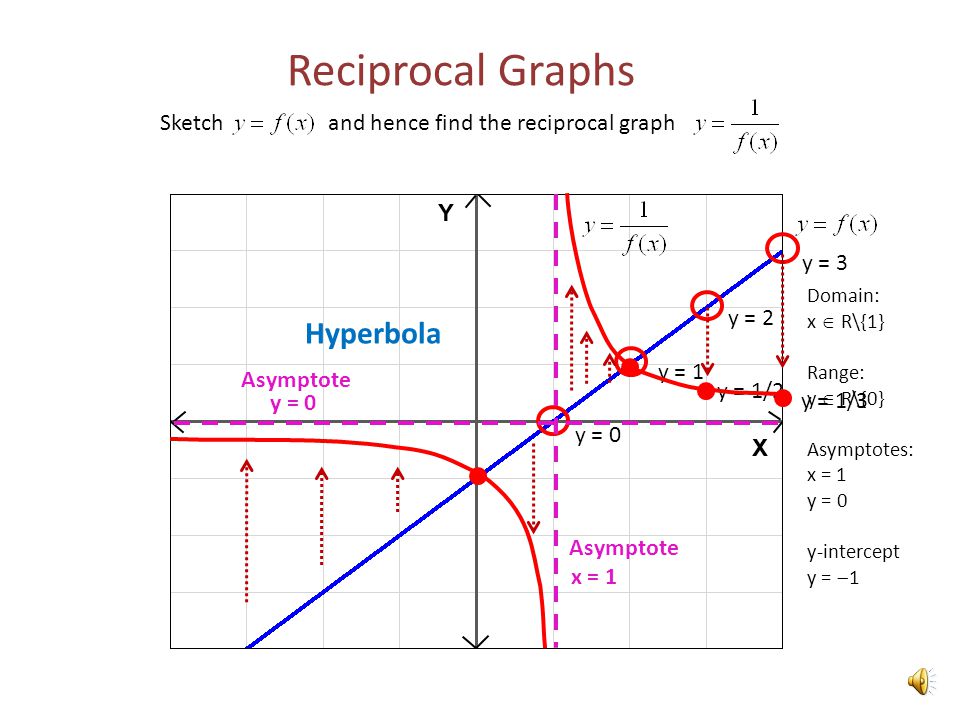
Reciprocal Graphs Sketch And Hence Find The Reciprocal Graph Y 0 Y 1 Y 2 Y 1 2 Y 3 Y 1 3 X 1 Y 0 Hyperbola Asymptote Domain X R 1 Ppt Download

Simple and best practice solution for x/y=2/3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,Answer (1 of 3) {(xy)^3/2×(xy)^3/2÷(xy)^1/2×(xy)^3/2}^6 ={(xy)^3/2×(xy)^3/2× 1/(xy)^1/2 ×(xy)^3/2}^6 ={(xy)×(xy)^3}^6 ={(x^2y^2)(xy)^2}^6 =(x^2yStudents of a class are made to stand in a row If one student is extra in each row, there would be 2 rows less If one student is less in each row, there would be 3 rows more Find the number of students in each class

2

If Y X Is The Solution Of Dy Dx X 2 1 Y 2 Y 0 2 Then Y 3 Homeworklib

 x²y²=xy x²y²xy=0 (x²xyy²)=0 Multyplying by (xy) on both sides we get, (xy) (x²xyy²)= (xy)×0 By eq1 we get, x³y³=0 Hence x³y³=0 ahlukileoi and 2717 more users found this answer helpful If you want to graph on the TI specifically, you'll need to do some easy math x² (yx^ (2/3))² = 1 (y x^ (2/3))² = 1 x² y x^ (2/3) = ±√ (1 x²) y = x^ (2/3) ± √ (1 x²) Now you have Y in terms of X The TI series doesn't have a ± sign, though, so you'll need to graph the two equations as a list Type this in in YAnswered January 7 Author has 12K answers and 3509K answer views For the equation y'' 2y ( (y')^3) = 0 ,a solution is y = const Moreover , take y' = V y (x) then y'' = V' (y)V (y) and the equation becomes V'V 2yV^3 =0 and V V' 2yV^2 = 0 Obtain the solution y = const and other solutions from

Y X 3 1

What Is The Graph Of X 2 Y 3 X 2 2 1 Quora

See the answer See the answer See the answer done loading Given y' = xy^3 (1x^2)^1/2 , y (0)=1 find a) solution of given initial amount in explicit form b) determine the interval for solution Expert Answer (x 3)(y − 4) = 0 −12 A)The quantity in Column A is greater B)The quantity in Column B is greater C)The two quantities are equal D)The relationship cannot be determined from the information given Practice Questions Question 6See the answer y=x^3 y=0 x=1 about x=2 Best Answer 100% (5 ratings) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator

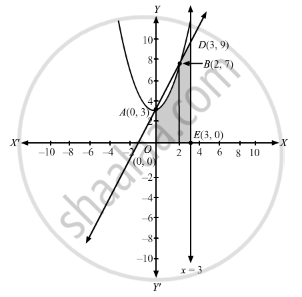
Make A Sketch Of The Region X Y 0 Y X2 3 0 Y 2x 3 0 X 3 And Find Its Area Using Integration Mathematics Shaalaa Com

Draw The Graph Of Y X 1 X 3 And Hence Solve X 2 X 6 0 Sarthaks Econnect Largest Online Education Community

Dx = Z 1 0 3x− 3x2 2!We could solve for the constant now 1 = C 2 −2, so C = 3 Solve for y y(x) = 1 q 3− √ x2 1 where we take the positive root since the initial condition was positive The solution will exist as long as the denominator is not zero Solving, 3−2 √ x2 1 = 0 √ x2 1 = 3/2 x = ± √ 5/2 The solution is valid for − √ 5 2 < x < √Values y1 0 1 y1 0 0 and y1 sinx is the solution with y1 0 0 y1 0 1 Then the solution with initial values y 0 and y 0 is (123) y x y 0 cosx y 0 sinx Example 122 Solve y y 0 with given initial values y 0 y 0 Now ex and e x are solutions of this differential equation, so the general solution is a linear combination of these

2

Answered 1 Two Discrete Random Variables X And Bartleby

C and the solution satisfies φ(x,y) = e2xy 2 x2 2 = C 4 (Sec 31 Problem 10) y00 4y0 3y = 0, y(0) = 2 and y0(0) = −1 Solution Solving r2 4r 3 = 0, we have r = −1 and r = −3 So y(t) = ce−t de−3t Using y(0) = 2, we have c d = 2 Now y0(t) = −ce − t−3de 3 Using y0(0) = −1, we have −c−3d = −1 Solving c Get an answer for '`y = x^3, y = 0, x = 1` Find the volume of the solid obtained by rotating the region bounded by the given curves about A Relation R is given by the set {(x, y)/y = x 3, x ∈ {0, 1, 2, 3, 4, 5}} Determine its domain and range

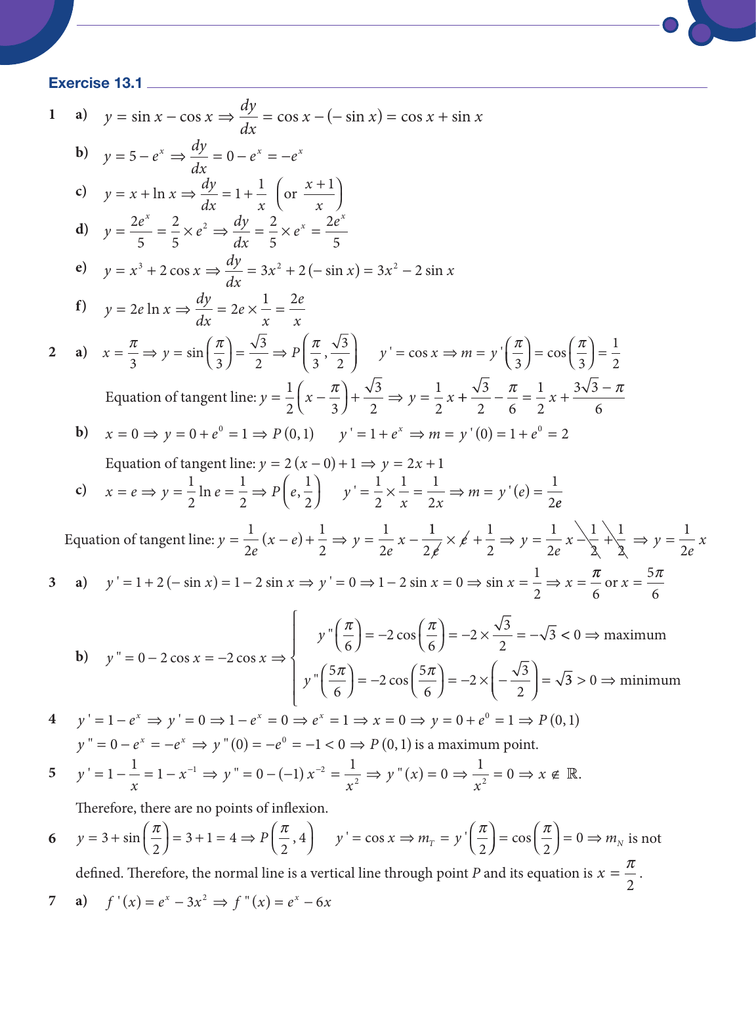
X X Dy Dx X X X X Sin Cos Cos Sin Cos Sin

Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange

MATH 15 Write a function rule that represents y is 5 less than the product of 4 and x 16 Write a function rule that represents 7 less than three fifths of b is a 17 Write a function rule that represents the Ex 21, 1 If (x/3 " 1, y –" 2/3) = (5/3 "," 1/3) , find the values of x and y (x/3 " 1, y –" 2/3) = (5/3 "," 1/3) Since the ordered pairs are equal, corresponding elements are equal Hence x/3 1 = 5/3 x/3 = 5/3 – 1 x/3 = 2/3 x = 2 y – 2/3 = 1/3 y = 1/3 2/3 y = 3/3 y = 1 Show MoreEasy as pi (e) Unlock StepbyStep Natural Language

Find The Area Of The Shaded Region X Y 2 1 Y 1 X Sqrt Y Mathematics Stack Exchange

Quadratic Graphs Parabolas 1 To Draw A Quadratic

You must use the "*" (star) symbol for all multiplications!x(x1) is WRONG!Y=x^3 Y=0 X=1 About X=2;Simple and best practice solution for x^3y^3x^2y^2=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework

Example 15 Find Area X Y 0 Y X2 1 0 Y X 1

4a Volume Of Solid Of Revolution By Integration Disk Method

 Corresponding elements are equal Therefore, 2 y = 5 2x 2 = 8 Solving (1) 2 y = 5 y = 5 2 y = 3 Solving (2) 2x 2 = 8 2x = 8 2 2x = 6 x = 6/2 = 3 Hence x = 3 & y = 3 Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at TeachooSolve by Substitution 2xy=3 , xy=0, Subtract from both sides of the equation Replace all occurrences of with in each equation Tap for more steps Replace all occurrences of in with Simplify Tap for more steps Multiply by Subtract from Divide each term by and simplifyIf $x = 1$, then $x^2xyy^3 = 1$ gives $yy^3 = 0 \implies y(y^21) = 0 \implies y = 0$ In the first step, we get $$2y' = 0 \implies y' = 2$$ Now we sub $x = 1, y = 0, y' = 2$ in the second step, to get $$24y'' = 0 \implies y'' = 2$$ Plugging all in the last step $$44y''' = 0 \implies y''' = 42$$

14 5 Directional Derivatives

Draw A Rough Sketch Of The Given Curve Y 1 X 1 X 3 X 3 Y 0 And Find The Area Of The Region Bounded By Them Using Integration Studyrankersonline

Solve the Following Pair of Linear (Simultaneous ) Equation Using Method of Elimination by Substitution 2( X 3 ) 3( Y 5 ) = 0 5( X 1 ) 4( Y 4 ) = 0 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions 145 1 yes 2 no 3 (4,0) & (3,1) 4 96 5 3y6=5y8 6 An equation can be used to predict values from a pattern by merely substituting any value to determine the equivalent value An example is the geometric series which has a standard equation of an = a1 * r^(n1) and is used to predict the nth term of the series 7 Price # of pizzas 1)50 1 3)00 2 4 A firstorder approximation to the arc length gives 8tan^(1)(2sqrt3) units >y=x^3 y'=3x^2 Arc length is given by L=int_0^2sqrt(19x^4)dx Apply the substitution sqrt3x=u L=1/sqrt3int_0^(2sqrt3)sqrt(1u^4)du Complete the square in the square root L=1/sqrt3int_0^(2sqrt3)sqrt((u^21)^22u^2)du Factor out the larger piece L=1/sqrt3int_0

Solved 6 2 Exercises 15 Y X Y 0 X 1 About X 1 18 Find Chegg Com

Engineering Mathematics Ii Pages 151 0 Flip Pdf Download Fliphtml5

How to solve and grah this equation y=x^3 1 If x=2 y=(2)^31 y=81 y=7 Plot (2,7) If x=1 y=(1)^31 y=11 y=0 Plot (1,0) If x=0 y=(0)^21 y=1 Plot (0,1) If x=1 y=(1)^31 y=11 y=2 Plot (1,2) If x=2 y=(2)^31 y=81 y=9 Plot (2,9) Connect your points and you have If you know what the graph of y=x^3 looks like, it's exactly theSOLUTION 1 Begin with x 3 y 3 = 4 Differentiate both sides of the equation, getting D ( x 3 y 3) = D ( 4 ) , D ( x 3) D ( y 3) = D ( 4 ) , (Remember to use the chain rule on D ( y 3) ) 3x 2 3y 2 y' = 0 , so that (Now solve for y' ) 3y 2 y' = 3x 2, and Click HERE to return to the list of problems SOLUTION 2 Begin with (xy) 2 = x y 1 Differentiate both sidesHow many are wrong?

1

Graph Graph Equations With Step By Step Math Problem Solver

 The general solution of the differential equation √(1 x^2 y^2 x^2y^2) xy(dy/dx) = 0 is (where C is a constant of integration) asked in Mathematics by Anjali01 (476k points) jee main 1 vote 1 answer Let y = y(x) be the solution of the differential equation cosx dy/dx 2y sin x = sin 2x, x ∈ (0, π/2) If y(π2x35x2yxy26y3 Final result 2x3 5x2y xy2 6y3 Step by step solution Step 1 Equation at the end of step 1 (((2•(x3))((5•(x2))•y))(x•(y2)))(2It means a function x of x1x*(x1) is rightUse the ^ (caret) for exponentiation x^2 means x squared x/2y means Resources Simplifier Portal, help with entering simplifier formulas (a must read)

Y X 2 1 Y 0 X 2 X 3 Magreig

How To Find Algebraically And Graphically The Points Where The Line X Y 1 0 Meet Y Axis And X Axis Quora

1/x 1/y = 1/3, 1/x^2 1/y^2 = 5/9 squaring both sides of 1/x 1/y = 1/3 and substituting value of 1/x2 1/y2 = 5/9, we get 2/xy = 4/9 Find value of 1/x1/y using formula (1/x1/y)^2= (1/x 1/y )^2 4/xy Then 1/x 1/y =1 solving these , we get x= 3/2 and Y= 3 Is this solution Helpfull?Solve 2xy/ X Y = 3/2 Xy/ 2x Y = 3/10 X Y ≠ 0 and 2x Y ≠ 0 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions 145 Concept Notes & Videos 431 Syllabus Advertisement Remove all ads Solve 2xy/ X Y = 3/2 Xy/ 2x Y = 3/10 X Y ≠ 0 and 2x Y ≠ 0 0 Office_Shredder said (xy) 2 = x 2 2xy y 2 >= 0 You know that already So x 2 xy y 2 >= xy If x and y are both positive, the result is trivial If x and y are both negative, the result is also trivial (in both cases, each term in the summation is positive) When one of x or y is negative, xy becomes positive

If Y X Is The Solution Of Dy Dx X 2 1 Y 2 Y 0 2 Then Y 3 Homeworklib

Solve In Series The Equation 1 X 2 D 2y Dx 2 X Dy Dx Y 0 About The Point X 0 Mathematics 2 Question Answer Collection

This problem has been solved!The answer is, not really It is still always going to be implicit Given x = r*cos (θ) and y = r*sin (θ), the equation posted reduces to (r2 1)3 = r5 cos2 (θ) sin3 (θ) Thats about as simple as I could get it To the first order you can solve for θ to get ** θ = r 2/3 r 5/3 ** 9 Continue this thread level 2Question Y=x^3 Y=0 X=1 About X=2 This problem has been solved!

2

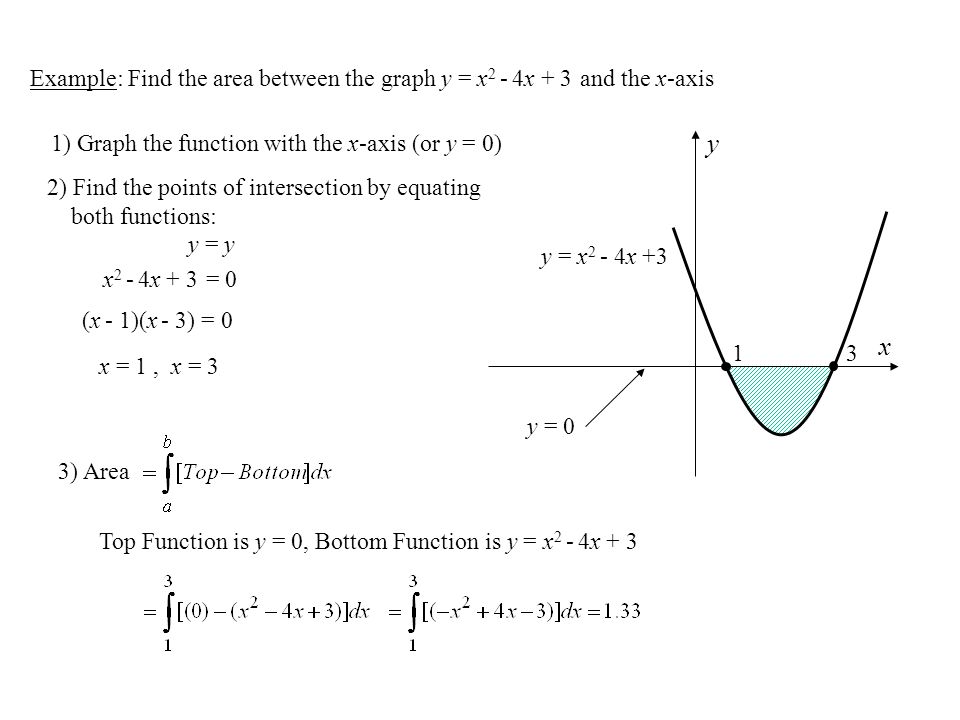
Section 5 3 Finding The Total Area Shaded Area Ab Y F X X Y Y G X Ab Y X Shaded Area Ppt Download

 Best Answer #2 299 10 The distance formula (actually, the Pythagorean Theorem) that gives the distance between the points (x 1, y 1) and (x 2, y 2) is d = √ (x 2 x 1)2 (y 2 y 1) 2 The distance from x (1, 3) and y (3,0) call x 1 = 1, y 1 = 3, x 2 = 3, y 2 = 01 2 3\pi e x^{\square} 0 \bold{=} Go Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem xy'y=x^{2}2x1 en Related Symbolab blog posts Advanced Math Solutions – Ordinary Differential Equations Calculator, Exact Differential EquationsCancel the common factor Divide ( x − 3) ( x 1) ( x 3) ( x 1) by 1 1 Divide 0 0 by 2 2 If any individual factor on the left side of the equation is equal to 0 0, the entire expression will be equal to 0 0 Set the first factor equal to 0 0 and solve

Content Newton S Method

Graph The Linear Equation Yx 2 1 Draw

(3−x−y)dA = Z 1 0 Z x 0 (3−x−y)dydx = Z 1 0 " 3y −xy − y2 2 # y=x y=0 dx = Z 1 0 3x−x2 − x2 2!If y=0 , then so that 2x 23x=x(2x3)=0 Thus, x=0 and x=3/2 are xintercepts There is no horizontal asymptote since , and Remember, a horizontal asymptote exists only if the limit to or is a finite number Now check for a vertical asymptote by computing onesided limits at the zero of the denominator, ie, at x=2 Thus, X 3, 2, 1, 0, 1 Y 1, 2, 5, 8, 11 How do I find the answer?

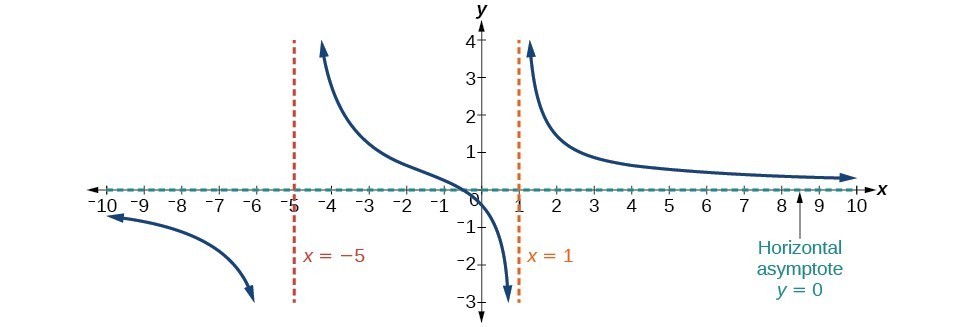
Horizontal Asymptotes And Intercepts College Algebra

Solutions To Implicit Differentiation Problems

Pozhalujsta Pomogite Vychislit Ploshad Figury Ogranichennoj Liniyami Y 1 X3 Y 0 X 1 Znaniya Online

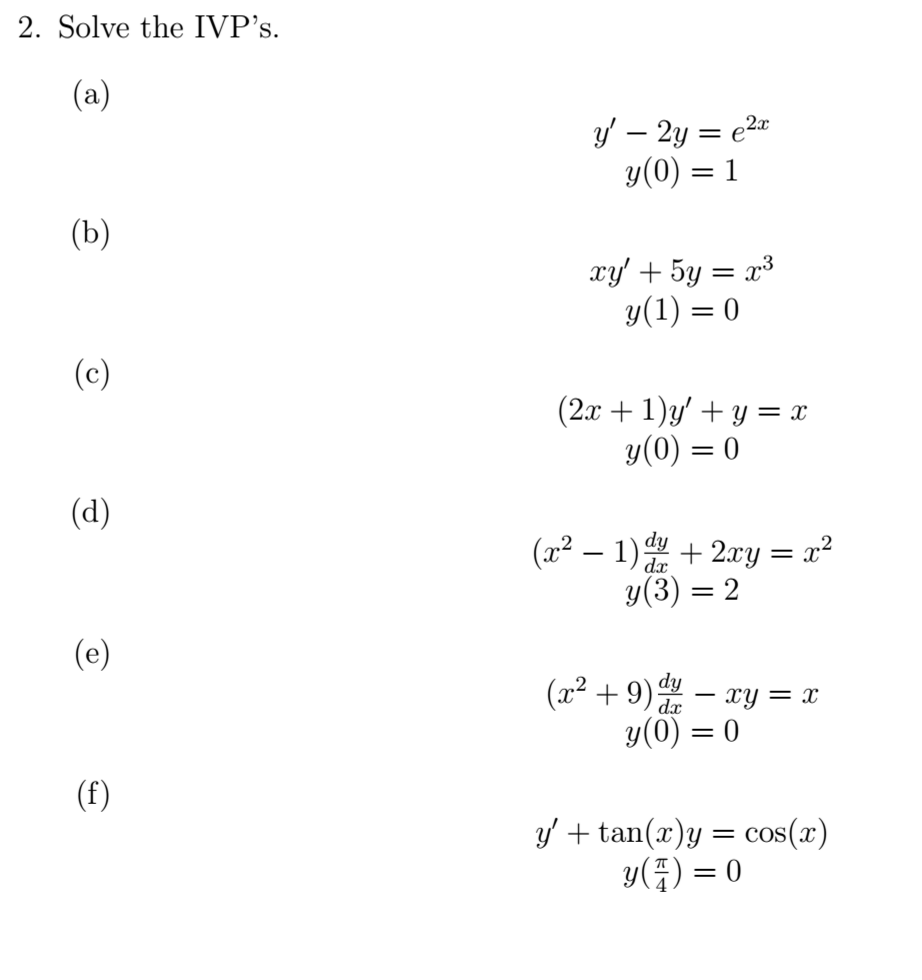
Solved Solve The Ivp S Y 2y E 2x Y 0 1 Xy 5y Chegg Com

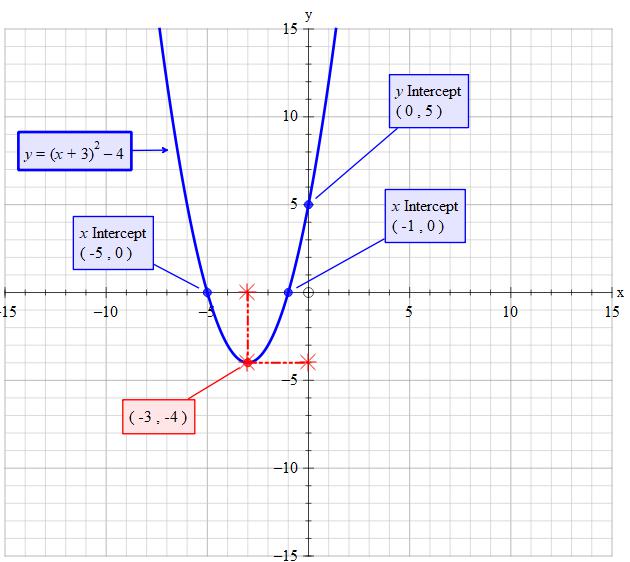
How Do You Find The Vertex And Intercepts For Y X 3 2 4 Socratic

Find Equation Of Tangent To Y X 3 1 X 2 Find Interval Where

Graph Graph Equations With Step By Step Math Problem Solver

15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts

Quadratic Function

Quadratics

2

Math Spoken Here Classes Quadratic Equations 3

Mathematics Ii Tranquileducation

Solve 2 X 2 3y 1 6 And 3 X 2 Y 0 And Hence Find A For Which Y A X 4

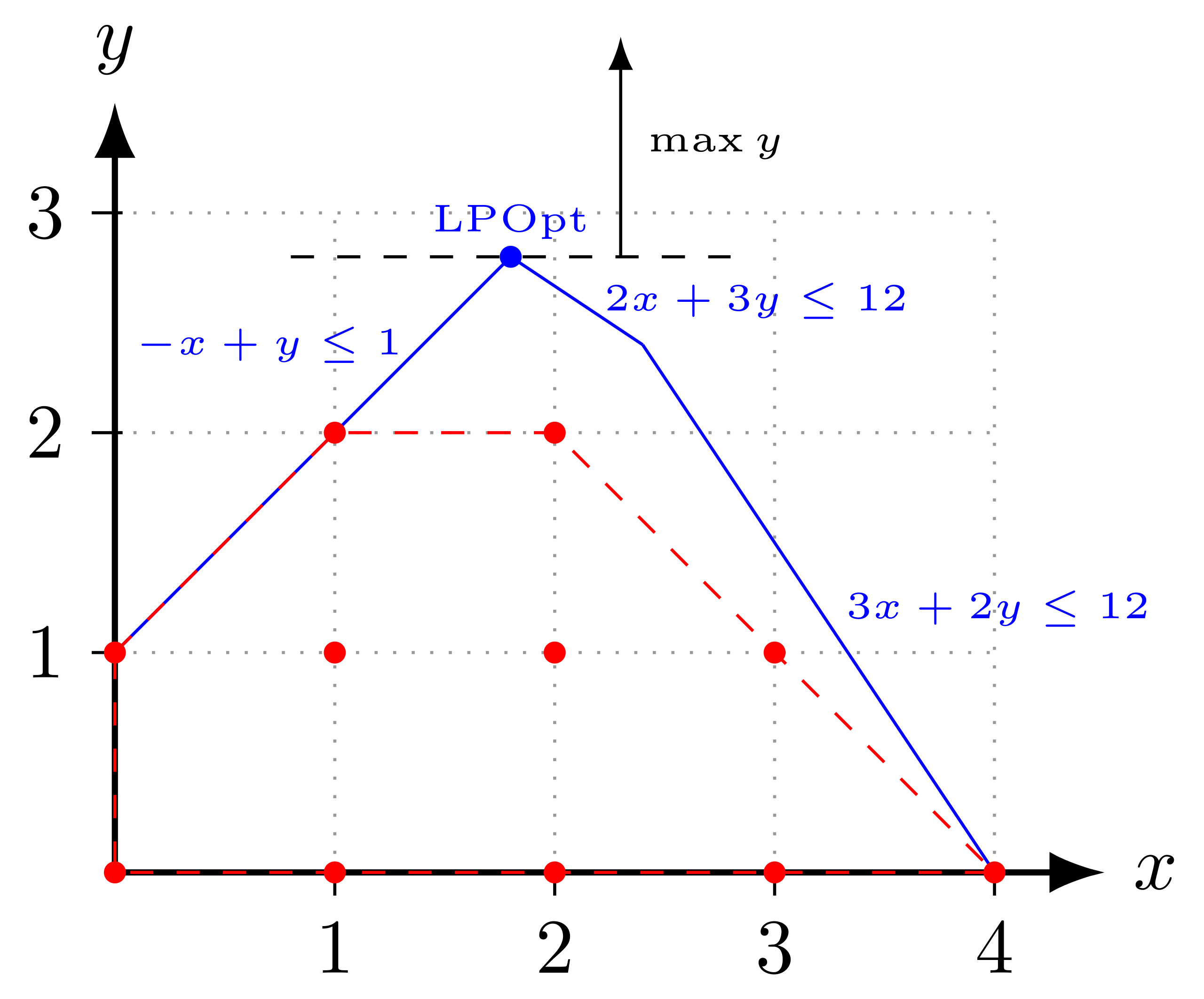
Integer Linear Programming Apmonitor

Math Spoken Here Classes Quadratic Equations 3

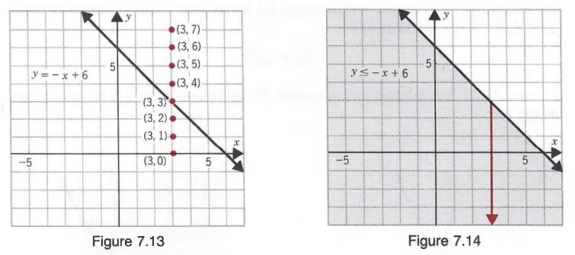
Graph Graph Equations With Step By Step Math Problem Solver

2

First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download

2

Ex 3 2 7 Draw Graphs Of X Y 1 0 And 3x 2y 12 0

Pyplot Tutorial Matplotlib 3 4 3 Documentation

Solution I Am Having Trouble With Trying To Figure Out How To Graph Y X 1 Y X 3 To Get 2 1

Average Value And Area Revisited

Systems Of Linear Equations

2

2

6 4 Factoring And Solving Polynomial Equations Factor

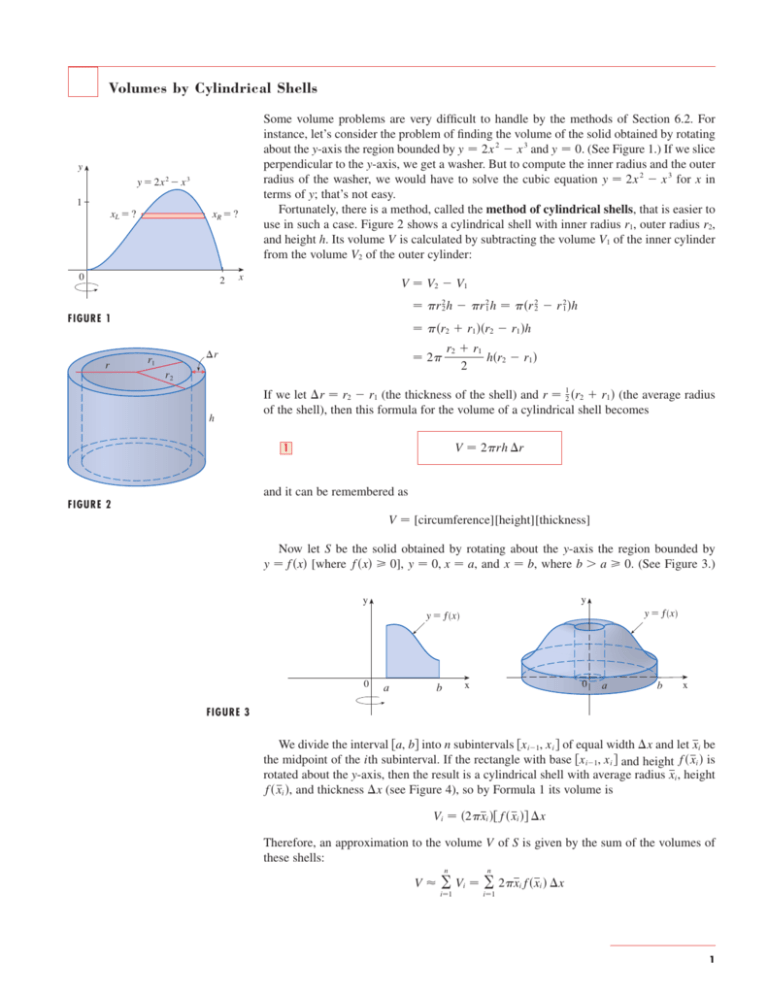
Volumes By Cylindrical Shells

How Do We Solve X 2 Y 2 10 1 X 1 Y 4 3 Quora

Engineering Mathematics Ii Pages 151 0 Flip Pdf Download Fliphtml5

Solution Y 5x 3 With Y 2x Find The Solution Of Each System Of Simultaneous Equations By Graphing

Solution Can We Sketch The Graph Of Y X X 1 X 4 Thinking About Functions Underground Mathematics

Graph Graph Inequalities With Step By Step Math Problem Solver

Y 1 2 Y 1 2 Y 1 Y X 2 X Y Y 1 2 Y 3 1 3 Ppt Download

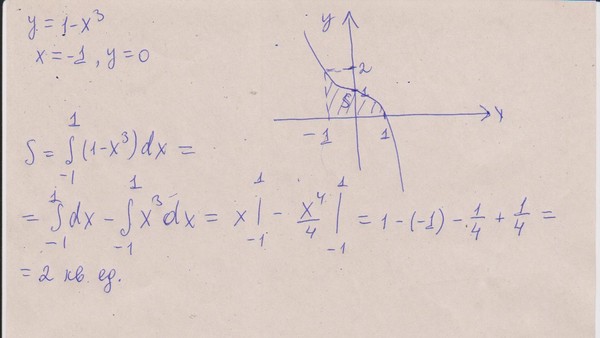
Otvety Mail Ru Pomogite Vychislit Ploshad Figury Ogranichennoj Liniyami Y 1 X 3 Y 0 X 1

Graphing Parabolas

2

Line Geometry Wikipedia

2

The Substitution Method

Solved Solve The De Y Xy X 2 1 Y 0 Find The Chegg Com

Find The Volume V Of The Solid Obtained By Rotating The Region Bounded By The Given Curves About The Specified Line Wyzant Ask An Expert

Parabola

Y X 2 6x 7

Y 1 X

2 X 2 3y 1 6 And 3 X 2 Y 0 Problem Set 1 Q6 1 Of Linear Equation In Two Variables Youtube

2

Graph Using Intercepts

Y X 2 3 X 1 Y 0 About The Y Axis Youtube

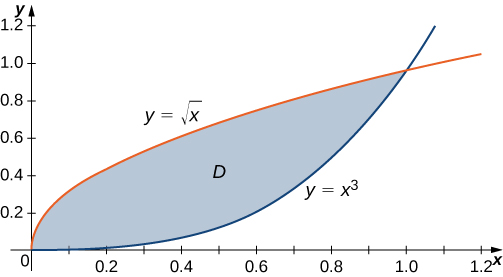
Double Integrals Over General Regions Calculus Volume 3

4a Volume Of Solid Of Revolution By Integration Disk Method

1 Consider The Following Equations Y X 2 4 Y X 5 X 0 X 2 Sketch And Shade The Region Bounded By The Graphs Of The Functions

1 1 Area Between Two Curves Mathematics Libretexts

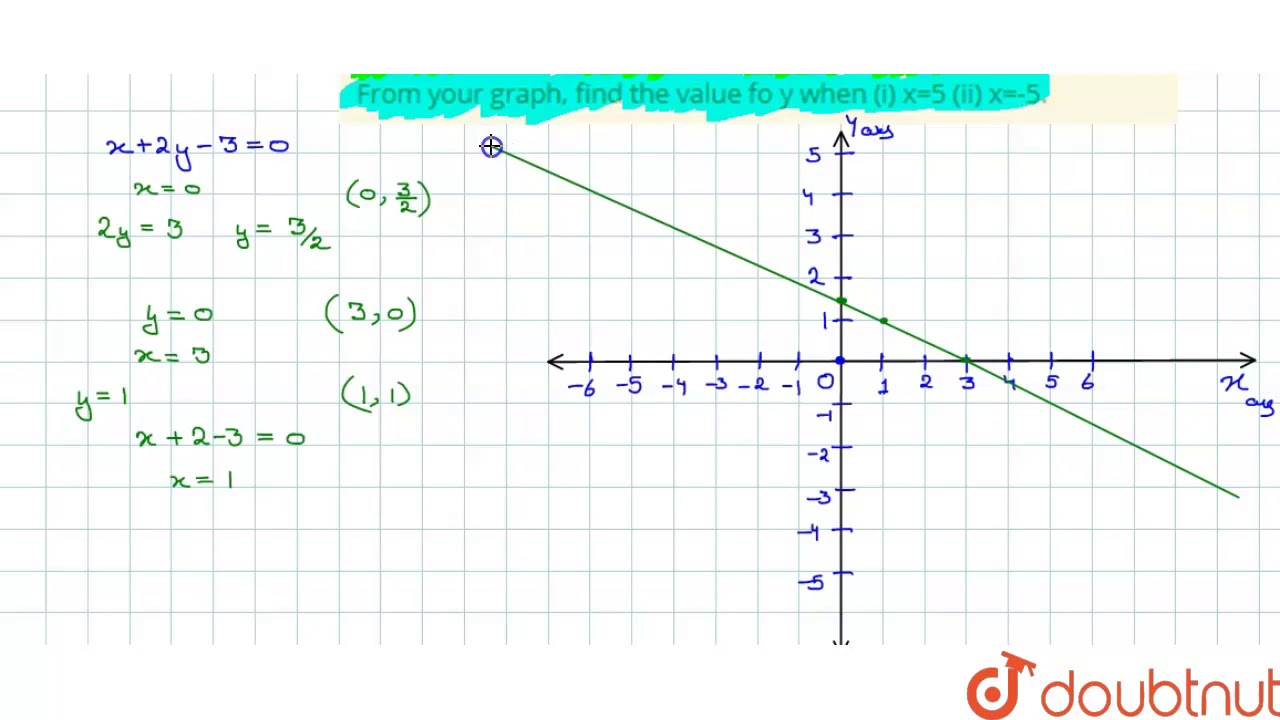
Draw The Graph Of The Equation X 2y 3 0 From Your Graph Find The Value Fo Y When I X 5 I Youtube

How To Solve Lim X Y To 0 0 Frac X 3 X 2 Y 2 Mathematics Stack Exchange

Bktpjofacbhsym

Solved 15 Y X Y 0 X 1 About X 2 2 16 Xy 1 Y Chegg Com

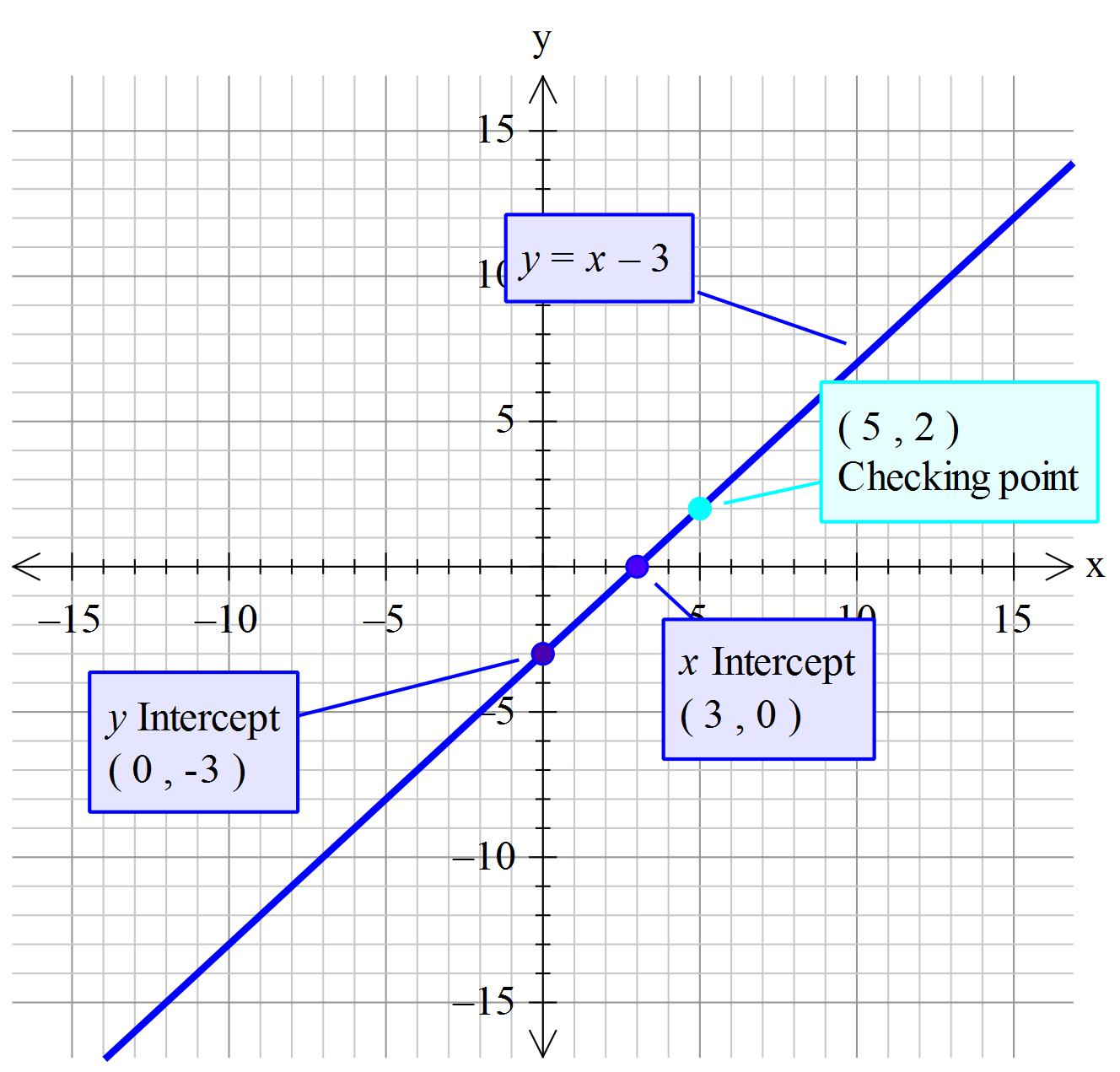
How Do You Graph Y X 3 Example

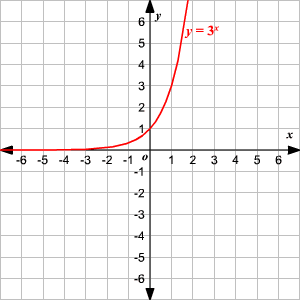
Graphing Logarithmic Functions

Linear Algebra Sheet 5 Summer 19 Warning Popup Annotation Has A Missing Or Invalid Parent Studocu

Math 432 Hw 2 5 Solutions

Finding Linear Equations

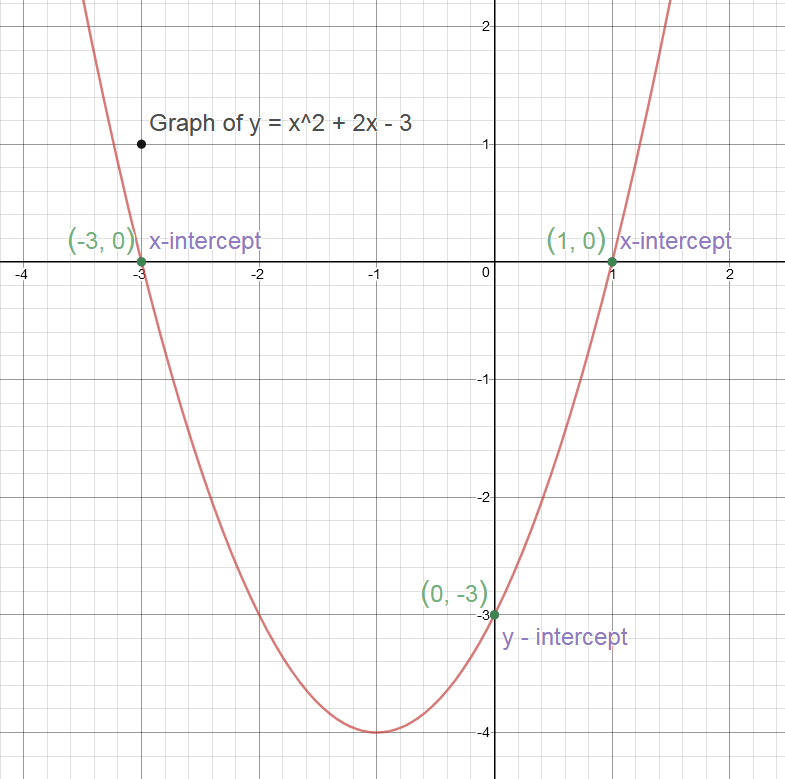
How Do You Find The X And Y Intercepts For Y X 2 2x 3 Socratic

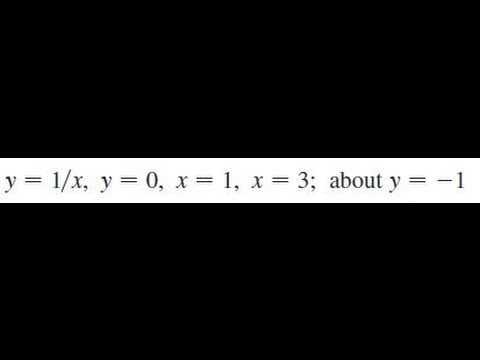
Y 1 X Y 0 X 1 X 3 About Y 1 Youtube

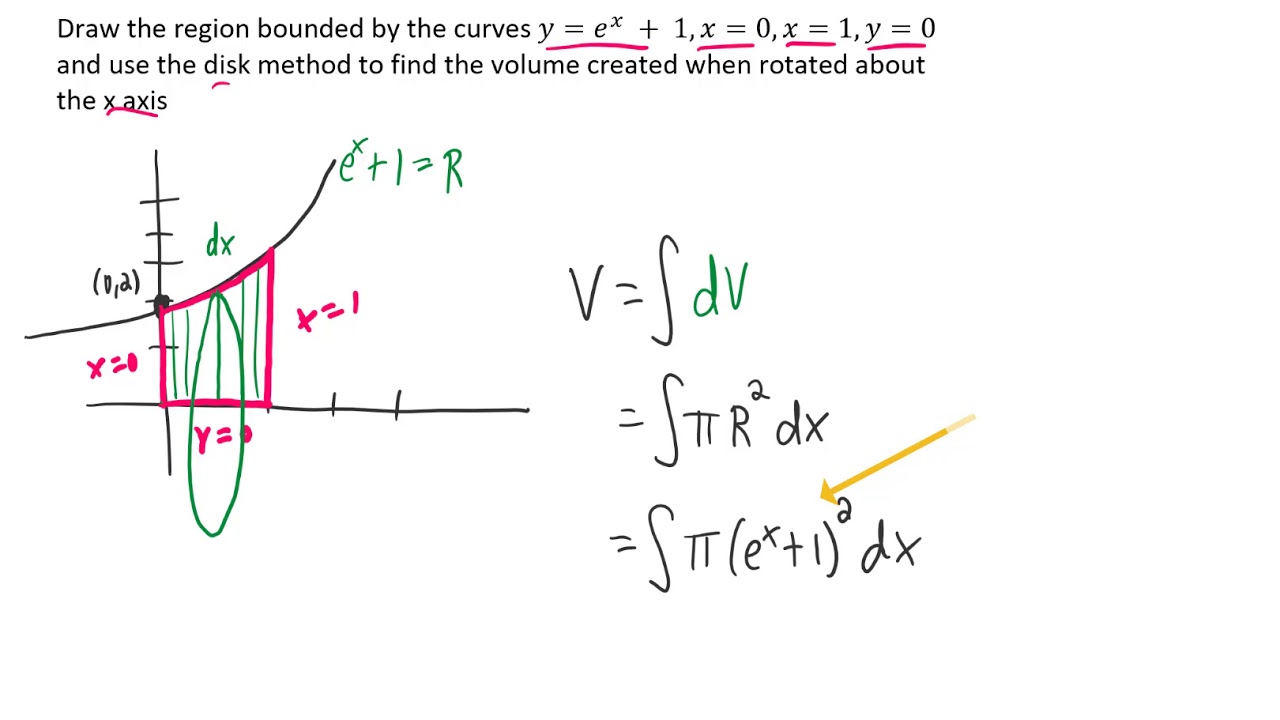
Draw The Region Bounded By The Curves Y E X 1 X 0 X 1 Y 0 And Use The Disk Method To Find The Youtube

1

Calc 501 1000 By James Bardo Issuu

Evaluate The Volume Of The Solid Bounded By Z 8 X 2 Y 2 Z X 2 Y 2 X 1 Y Sqrt 3 X Y 0 Mathematics Stack Exchange

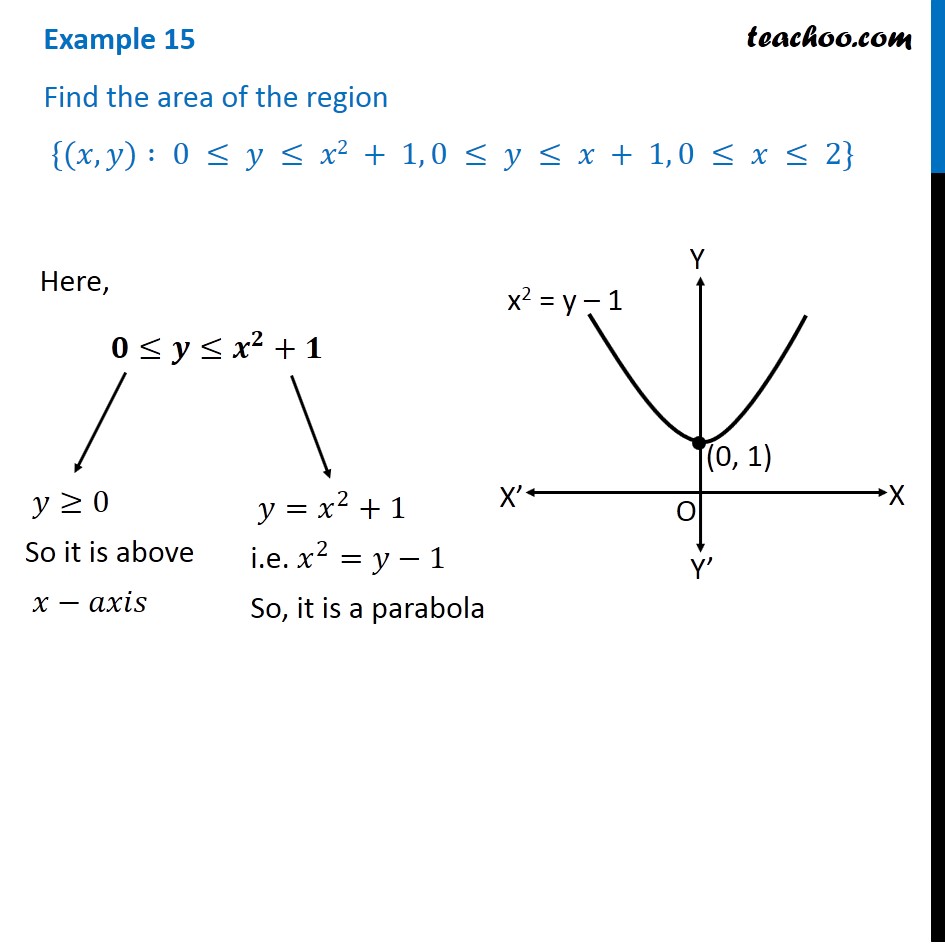
Example 15 Find Area X Y 0 Y X2 1 0 Y X

Draw The Graph Of The Equation 2 X 3 3 1 Y 0 Also Find The Point Where The Line Meets X Axis Mathematics Topperlearning Com 9107

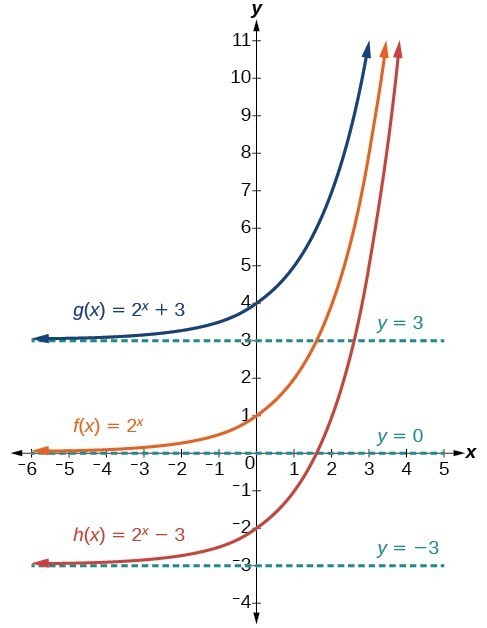
Graph Exponential Functions Using Transformations College Algebra

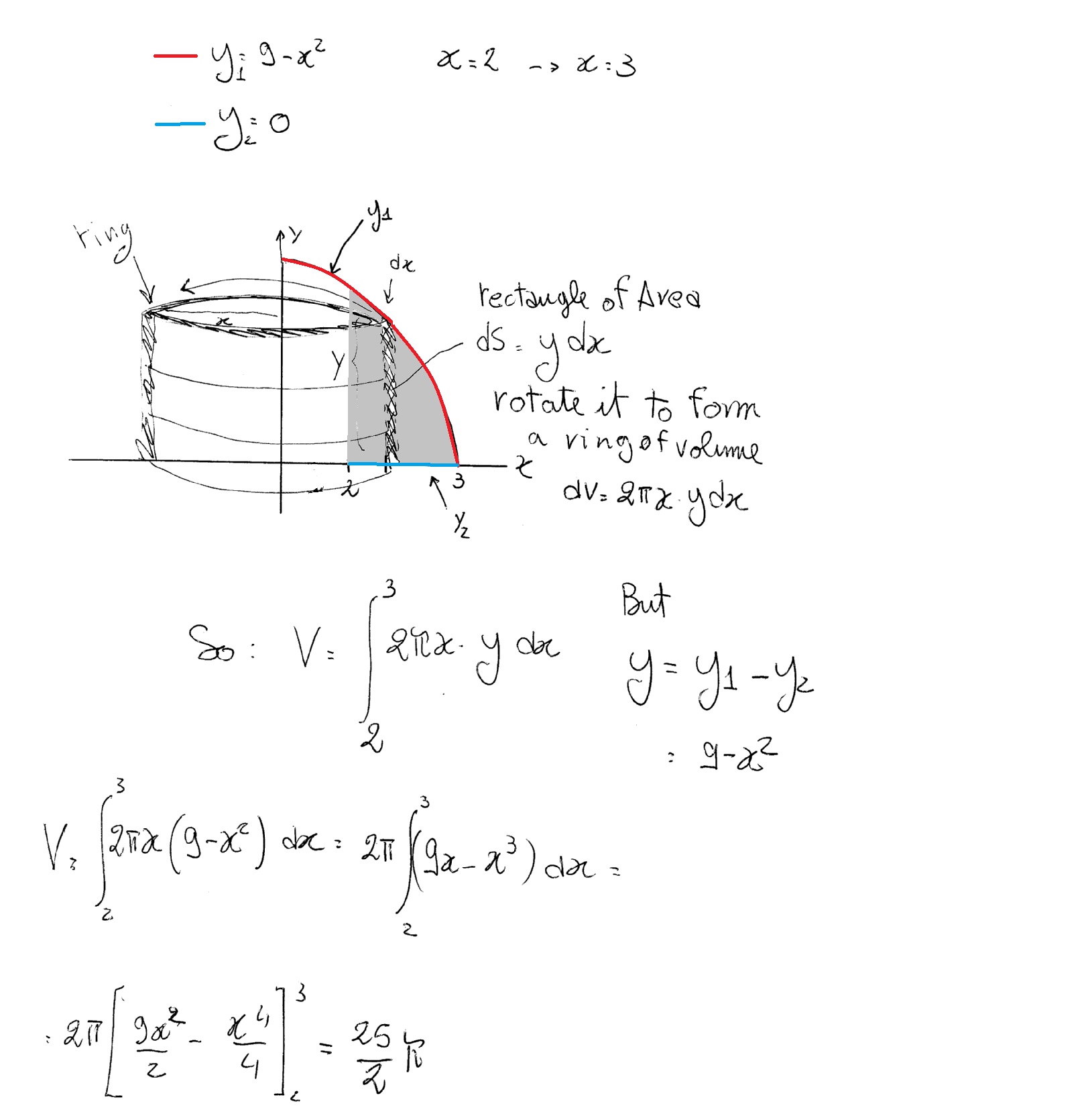
How Do You Find The Volume Of The Solid Generated By Revolving The Region Bounded By The Graphs Y 9 X 2 Y 0 X 2 X 3 About The Y Axis Socratic

Solved Solve The Initial Value Problem Y X 3 1 Y Chegg Com

Incoming Term: y x3 1 y 0 x 0 x 2,